Le petit précis des tracés régulateurs – La grille de 7
Sommaire :
Le site GASPARDDESTRE.com prend la relève !
Après 5 ans de bons et loyaux services, atelierdelame.fr ne sera plus mis à jour à partir du mois de septembre 2020.
Le tracé de la grille de 7 (G7)
Comment tracer la grille de 7
Pour tracer la grille de 7, une série de lignes supplémentaires sont à dessiner à partir des diagonales des doubles carrés.
Elles ont comme point de départ les angles du carré horizontal et passent par des intersections de diagonales des doubles carrés internes.
Ces intersections sont matérialisées dans la figure 1 par des petits carrés noir.
Elles sont à chaque fois la rencontre de diagonale d’un double carré vertical et et d’un double carré horizontal.
En partant du centre du carré, on relie les quatre premiers points qui formalisent une croix.
Ensuite, on relie les points situés sur le carré sur pointe en bleu sur la figure 2.
Vous remarquerez que les lignes passant par ces points alternent entre horizontal et vertical .

La grille de 7 et le triangle 3-4-5
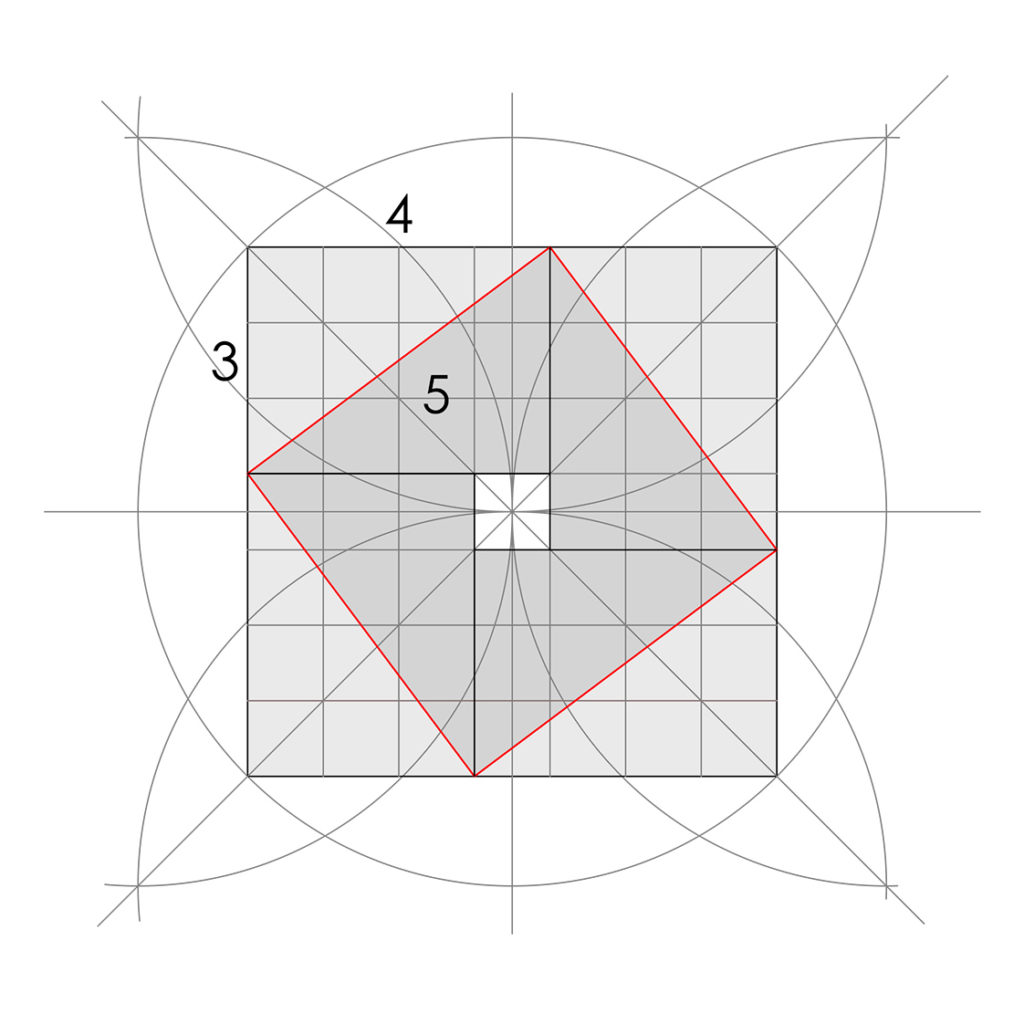
La grille de 7 met en évidence le triangle 3-4-5, tout comme la grille de 4.
Comme le montre l’image de la figure 3[1], le triangle 3-4-5 est issu des diagonales d’un rectangle de longueur 4 et de largeur 3.
Par ailleurs, la figure 3 souligne l’aspect impair de la grille de 7 par l’existence d’un carré central et le non marquage de la croix des orientations cardinales que l’on retrouve dans les grilles paires.
Les diagonales du carré dont les côtés sont les hypoténuses du triangle 3-4-5 sont égales à la racine carré de 50 (7² + 1²= √50). (fig.4)

Notes
[1] – Pour ne pas surcharger le dessin, les figures montrent seulement le carré dextrogyre. Bien sûr, les mêmes caractéristiques apparaissent avec le carré lévogyre.

 Article Précédent
Article Précédent Article Suivant
Article Suivant



